
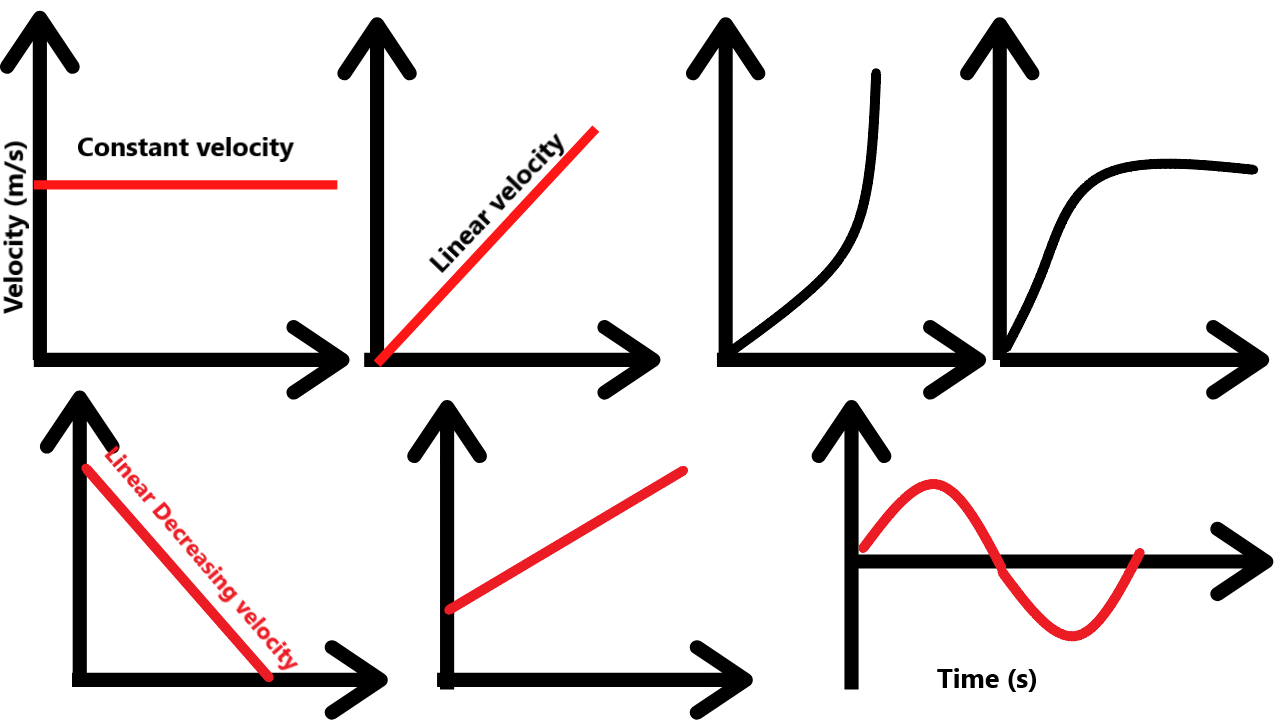
It is travelling at a '''constant velocity''' of '''+2ms^-1^'''ĭuring ''''Part B'''' of the journey the object travels '''0m''' in '''3s'''. For instance.ĭuring ''''Part A'''' of the journey the object travels '''+8m''' in '''4s'''. When describing the motion of an object try to be as detailed as possible. In Physics, we specify the origin landmark at 0 and the points either side of it are either positive or negative numbers (in units of metres).

Now left or right is not a good distinction as not everyone can agree with it. 5 metres from the door does not mean anything without giving some indication of direction (inside or out for example). Along a straight line, you only need the position of the landmark and how far the object is from the landmark left or right (or east or west). To describe the position of a moving object, you have to specify its position relative to a particular point or landmark that is understood by everyone.
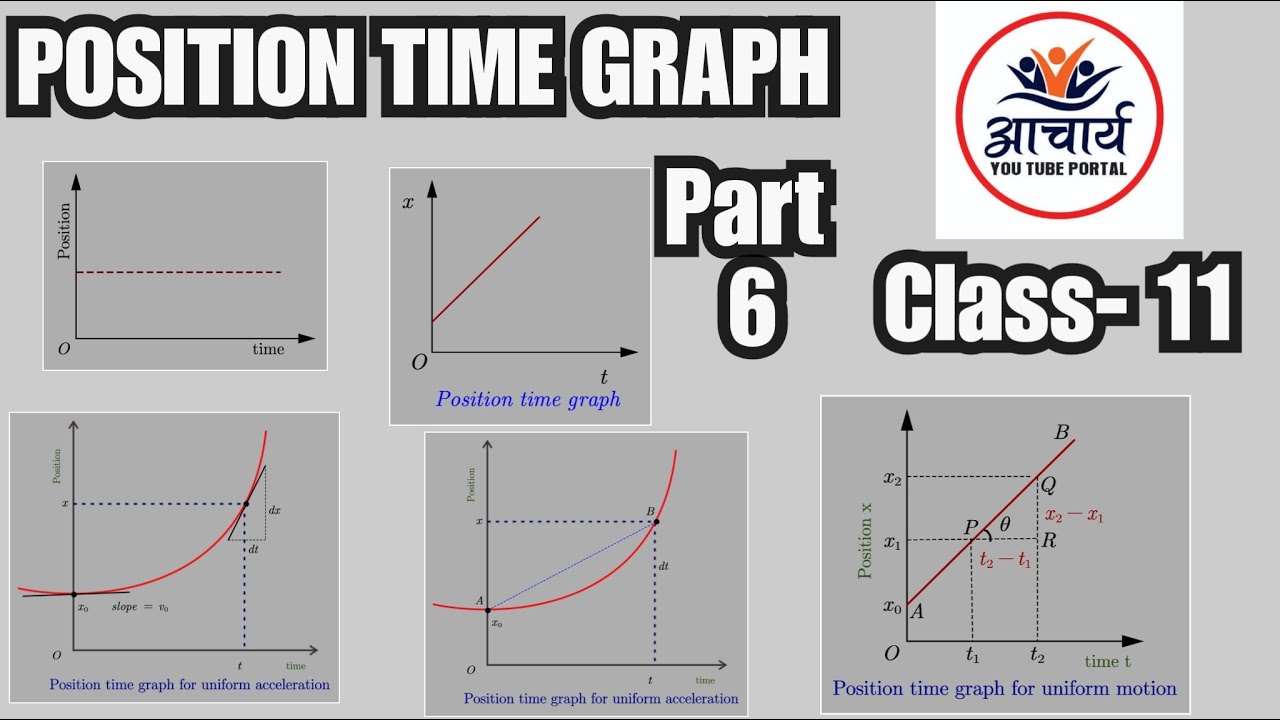
Will two cars crash if they are heading towards each other as they apply brakes at a certain time? In most mechanical problems we are asked to determine the connection between speed, position and time. This cannot be shown on a distance-time graph. Usually, a line with a negative gradient would indicate motion going backwards. Its distance would be the total length of the journey.Ī displacement-time graph is able to show if an object is going backwards or forwards. If an object goes back to where is started in certain time, then its displacement is zero. ''''Displacement'''' is the length between start and stop positions and includes a direction. Therefore '''Δt''' means '''"change in time"''' The '''Δ''' is just short hand for '''"change in"'''. You may also notice that the formula for calculating speed is sometime written with small triangles '''Δ''' (the Greek letter delta) in front of '''d''' (distance) and '''t''' (time). You can even do this for a curved line where the speed is changing, just remember that your result is the '''average''' speed in this case. The average speed can be calculated for any part of a journey by taking the change in '''distance''' and dividing by the change in '''time''' for that part of the journey. =Calculating Speed from a Distance-Time Graph= You can see that the distanced moved through each second is changing. The object is either getting faster = ''''accelerating'''' or slowing down = ''''decelerating''''. ''''Curved lines'''' on a distance time graph indicate that the speed is changing. A moving object is always ''''increasing'''' its total length moved with time. On a distance-time graph, there are no line sloping downwards. Note that you can think of a stationary object (not moving) as travelling at a constant speed of 0 m/s. ''''Straight lines'''' on a distance-time graph tell us that the object is travelling at a '''constant speed'''. The standard unit is the ''''metre''''.Ī distance-time graph shows how far an object has travelled in a given time.ĭistance is plotted on the Y-axis (left) and Time is plotted on the X-axis (bottom).īelow you can see that the object represented by the blue line has travelled 10m in 2s whereas the object represented by the red line has only travelled 4m in this time and is therefore travelling more slowly. Further information is provided in our Health and Safety guidance.''''Distance'''' is the total length travelled by an object. eLibrary users are responsible for ensuring that any activity, including practical work, which they carry out is consistent with current regulations related to Health and Safety and that they carry an appropriate risk assessment. Do NOT follow suggestions which conflict with current advice from CLEAPSS, SSERC or recent safety guides. Whilst this list provides a source of information and ideas for experimental work, it is important to note that recommendations can date very quickly. If students are not confident with the difference between speed and velocity then this can cause some confusion.Drawing the graphs themselves can be a challenge with some students struggling to select correct scales and calculate areas under graphs and gradients.It can be difficult to connect a static image (graph) with a dynamic process (motion graph).(acceleration the rate of change of a rate of change). Acceleration is not simple idea: it is the rate of change of velocity, and velocity itself is the rate a change of distance.Some students fail to grasp the distinction between velocity and acceleration – to them it’s simply ‘motion’.Some of the conceptual challenges in this topic are: They should be able to draw and interpret both distance-time and velocity-time graphs. Students should know that the motion of an object can be represented and analysed graphically.


 0 kommentar(er)
0 kommentar(er)
